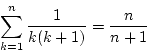
mpfrを利用した数値計算例
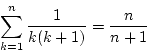
プログラム sum.cxx
indentation
1 #include 2 #include 3
4 #define LAST 1000
5 #define PREC 166
6
7 int main(void) {
8 mpfr_set_default_rounding_mode(GMP_RNDN);
9 mpfr_set_default_prec(PREC);
10 int k;
11 mpfr_class s;
12 mpfr_class a;
13 s = 0;
14 for(k=1; k 15 a = 1;
16 a /= k 17 s += a;
18 }
19 a = LAST;
20 a /= (LAST+1);
21 cout 22 cout 23 cout 24 }
g++ -o sum sum.cxx -lgmp -lmpfr
> ./sum
exact: 0.999000999000999000999000999000999000999000999000998e0
sum: 0.999000999000999000999000999000999000999000999000982e0
error: 0.160365882605531738768432188029088912728911812806303e-49
![]() までの総和
までの総和
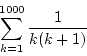
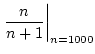 を直接計算した値を
比較すると、実行結果から誤差は
を直接計算した値を
比較すると、実行結果から誤差は
計算順序を入れ換えるなどの工夫をしなくても、簡単に高精度の計算結果を
得ることができる。
また、丸めの方法を変えることで制度保証計算を容易に行うことができる。