計算式の書き方
以下ではコンソール・ウィンドウでscilabのコマンドを直接実行してみる。プログラム中でもまったく同じように実行される。
四則演算(加減乗除)は普通の通りに式を入力する。
+ 足し算
- 引き算
* 掛算
/ 割り算
( ) 括弧
入力 1+1
結果 -->1+1
ans =2.
生まれてから何時間たったか計算してみよう。現在17歳ならば、以下で計算できる。
24×365.24×17
入力 24*365.24*17
結果 -->24*365.24*17
ans =149017.92
だいたい14万時間たったことがわかる。80歳まで生きるとすると80歳までの時間は70万時間だ。飲まず食わずに寝ないで映画を見続ければ35万本みられる。一冊10時間かけて読書をすると7万冊読める。
関数
高校で習った三角関数や指数関数も使うことができる。
ただし、この授業ではこれらの関数について高校で習ったことを知らなくても大丈夫。
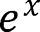
変数と代入
scilabでは変数に数値を保存して、後で使うことができる。
入力 x=1001
x*23
結果 -->x=1001
x =1001.
-->
-->x*23
ans =23023.
(-->図解)
配列
scilabでは変数に数字の列を代入することができる。
入力 t=[11,22,33,44,55]
t(3)=99
t(4)
結果 -->t=[11,22,33,44,55]
t =
11. 22. 33. 44. 55.
-->t(3)=99
t =
11. 22. 99. 44. 55.
-->t(4)
ans =
44.(-->図解)
数列
scilabでは 0:2:10というような表記をすることで、数列をあらわすことができる。
入力 0:2:10
0.5:0.7:3
結果
-->0:2:10
ans =
0. 2. 4. 6. 8. 10.
-->0.5:0.7:3
ans =
0.5 1.2 1.9 2.6
44.
累乗
累乗は、^ (山形)であらわす。^のキーはキーボードの0の2つ右にある。左側がベクトルの場合は .^ (点+山形)を使う。
入力 2^8
結果 -->2^8
ans =256.
入力 10^(-2) 結果 -->10^(-2)
ans =
0.01入力 [1,2,3,4].^2 結果 -->[1,2,3,4] .^ (-2)
ans =
1. 4. 9. 16.
さらに詳しく知りたい人のために
今日の授業ではここから以下の説明は省略する。数学が得意な人や、今日の授業と数学の関係をもっときちんと理解したい人は、後日ここから先を読んでおくとよい。
sin(1)は以下のようにして計算できる。
入力 sin(1)
結果 -->sin(1)
ans =0.8414710
平方根はsqrtでも計算できるが、1/2 乗しても計算できる。
入力 2^(1/2)
結果 -->2^(1/2)
ans =1.4142136
πは %pi であらわす
入力 cos(%pi)
結果 -->cos(%pi)
ans =- 1.
虚数単位 i = √-1 は %iであらわす。
入力 %i * %i
結果 -->%i * %i
ans =- 1.
オイラーの公式は以下のようにして確認できる。
入力 exp(%pi*%i)
結果 -->exp(%pi*%i)
ans =- 1. + 1.225D-16i
この時、答えは -1 にならず、 -1 + 1.225D-16iと表示される。1.225D-16iの D-16 というのは10のマイナス16乗、すなわち、0.000000000000001と等しい。非常に小さな値で、ほぼ0とみなしてよい数値であるから、実質的には答えは-1に限りなく近い。
しかしなぜ、わずかではあるが-1と差がでるのだろか。10進法で少数点を使って1/3を求め、3倍してもぴったり1にはならない。同じように、scilabではオイラーの公式を数値的に求めているため、ぴったり-1にならず、わずかではあるが誤差が残ってしまう。