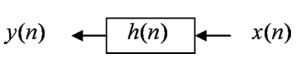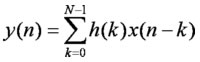インパルス応答とZ変換
さて、以前の講義でz変換について学んだ。
-> 第8回資料 の "4 Z変換" を参照
Z変換では数列をZの関数に変換した。そして、Z変換に関する表に、
という場合に、
[式3]
という項目があった。これは何だろうか。この行は
h(n)というインパルス応答がある伝送路をx(n)という信号が通って、その出力がy(n)の場合に、y(n)のZ変換が[式3]で求められることを表している。
本当にそうなるだろうか? 以下で計算してみよう。
h(n) = [1,1/2,-1/2,0,...]
x(n) = [1,0,0,-1,0,0,0,..]
だとすると、
をそのまま計算すると、
y(n) = 1 * [ 1, 0, 0,-1, 0, 0, 0,...]
+ 1/2 * [ 0, 1, 0, 0,-1, 0, 0, 0,...]
- 1/2 * [ 0, 0, 1, 0, 0,-1, 0, 0, 0,...]= [ 1, 0, 0, -1, 0, 0, 0,...]
+ [ 0,1/2, 0, 0,-1/2, 0, 0, 0,...]
+ [ 0, 0, -1/2, 0, 0,1/2, 0, 0, 0,...]= [1, 1/2,-1/2, -1,-1/2,1/2, 0, 0, 0, 0,...]
であるから
Y(z) = 1+z^(-1)/2-z^(-2)/2-z^(-3)-z^(-4)/2+z^(-5)/2
となる。
次にz変換を使ってY(z)を求めてみる。
H(z) = 1 + z^(-1)/2 -z(^-2)/2
X(z) = 1 - z^(-3)
だから、
Y(z) = H(z)X(z)
= (1 + z^(-1)/2 -z(^-2)/2) × (1 - z^(-3))
= 1+z^(-1)/2-z^(-2)/2-z^(-3)-z^(-4)/2+z^(-5)/2
で、たしかに、Y(z)=H(z)X(z)で計算しても同じ答えになることがわかる。
このようにインパルス応答と入出力の関係は、それらをz変換としておくと、掛け算という簡単な演算で表すことができる。