行列として理解する
離散フーリエ変換は、行列計算と考えることもできる。離散フーリエ変換の定義は(1)式だった。
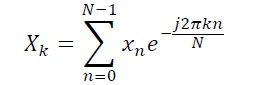 |
(1) |
ここで以下のような数 W を考える。Wは複素数である。
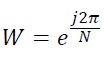 |
(2) |
Wを使うと式1は以下のように書ける
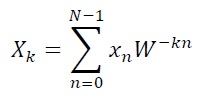 |
(3) |
そこでWを使った行列を考えると、x-->Xの変換は以下の(4)式の行列の計算でも計算できる。
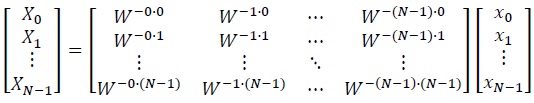 |
(4) |
本当にこの行列計算で同じ結果が得られるだろうか。
線形代数の行列の計算を思い出してみよう。以下のように行うのだった。
比較すると、確かに式(1)と式(5)は同じ計算であることがわかる。
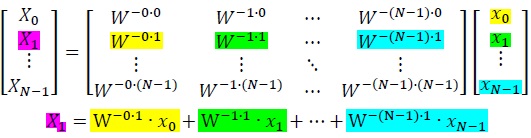 |
(5) |
離散フーリエ変換は行列の乗算としても計算できることがわかった。
同じデータをし, 式5でフーリエ変換して比較することで、確認しなさい。
この時のWの行列の要素は、単位円上の複素数で以下のように並んでいる。
このことから以下のことがわかる。
(1) この行列の基底は、すべて互いに直交している。
(2) この行列の基底の大きさは N
(3) DFTの結果の実数部分は左右対称
(4) DFTの結果の虚数部分は左右で符号が反対
(5) DFTと逆DFTは、逆行列
練習問題
x=[5,9,6,3,4,6,4,9]
という数列(ごくろーさん、よろしく)を作れ。
y=fft(x,1)で逆フーリエ変換せよ。
x1=fft(y,-1)でフーリエ変換せよ。
式(5)を使ったフーリエ変換を実行し、結果をx2に算出せよ。
x1とx2を比較せよ。