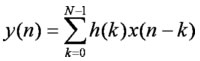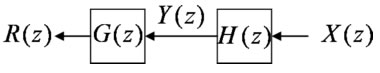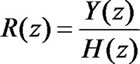Z変換と逆フィルター

h = [1,1,0,0,....]

というフィルタを考える。

たとえば、

x= [0,0,1,1,0,0,...]

ならば

により計算すると、

y= [0,0,1,2,1,0,0,...]

となる。このようなフィルターを通過して変形した波形を元に戻すことは可能だろうか?

このような問題はZ変換を用いて、解決することができる。

という処理を考えて、R(z)=X(z)となるG(z)を考えればよい。

Ｒ（ｚ）　＝　Ｇ（ｚ）Ｙ（ｚ）

なので

Ｇ（ｚ）　＝　Ｒ（ｚ）／Ｙ（ｚ）　＝　Ｘ（ｚ）　／　Ｙ（ｚ）

Ｙ（ｚ）　＝　Ｈ（ｚ）　Ｘ（ｚ）

だから

G(z) = 1/H(z)

となる。

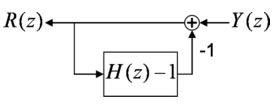
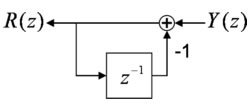
ところで、以下のような、フィードバックのある信号処理を考えてみる。

このとき Y(z)とR(z)の関係を計算すると、

となる。つまりフィードバックのある信号処理を行えば、その全体の伝達関数G(z)は

となることがわかる。

実際にやってみよう。

であれば

だから、G(z)は以下のような信号処理になる。

実際に

を入力し、Y(z), R(z), (H-1)Rを計算すると以下のようになる。

Y(z)	R(z)	(H-1)R
0	0	0
0	0	0
1	1	0
2	1	1
1	0	1
0	0	0
0	0	0
0	0	0

実際にこの例で R が Xと等しくなることが確認できた。