fftによる逆フィルター

逆フィルタを構成するには、

(1)Z変換の逆数を用いる方法

(2) fftの逆数を用いる方法

がある。

fftによる逆フィルターは、fftの以下の性質を用いている。

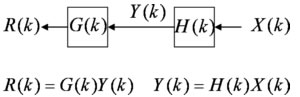
x(n)がフィルタh(n)を通った結果がy(n)であるとき

H(k)がh(n)のフーリエ変換

X(k)がx(n)のフーリエ変換

Y(k)がy(n)のフーリエ変換

であるならば、

Y(k)= H(k) ・ X(k)

つまり下図のようになる。

つまりz変換と同じように、フーリエ変換についても、信号をフィルターに適用したら、さらに別のフィルターを適用した場合に、出力信号にはフィルターのフーリエ変換が「乗算」されていく。

これを利用すると、以下の手順で逆フィルターを求めることができる。

step	式	目的
	l=1024	lをfftサンプル数とする(長いほど正確)
	h=...	変数hにインパルスレスポンスを求める
1	h(l)=0;	hを十分長い区間で定義する
2	h2=fft(h,-1);	hの周波数応答h2を求める
3	g2=1 ./ h2;	周波数応答の逆数=逆フィルターの周波数応答、を求める
4	g2=fft(h,1);	逆フィルターのインパルスレスポンスを求める

たとえば

h=[1,0.4,0.2,0.1]

というインパルスレスポンスに対する逆フィルターを求めてみよう。

インパルスレスポンスは最初に変数hに与え、逆フィルタのインパルスレスポンスを計算して変数gに代入している。

l=1024; h=[1,0.4,0.2,0.1]; h(l)=0; h2=fft(h,-1); g2=1 ./ h2; g=fft(g2,1);

元のフィルタ [1,0.4,0.2,0.1]と逆フィルタのインパルスレスポンスをプロットして比べてみる。

plot(h(1:10)); plot(g(1:10));

次に適当な信号をxに用意して、まずフィルタhを適用し、次にフィルタgを適用して結果をyに代入する。

x=[0,0,1,0,-1,0,0,0,0,0]; y=convol(h,x); r=convol(g,y); plot(x); plot(y(1:10)); plot(r(1:10));

フィルタをかけた信号yに逆フィルタgをかけた結果がxと等しいことがわかる。