音階の演奏
周波数を 2の n/12 乗倍することで半音音階を作ることができる。
stacksize(1e8); fs=44100; x=zeros(1:20*fs); w=0:10000; t=w/fs; for i=0:14 s=i*fs/4; n=i; f=440*2^(n/12); x(w+s+1)=x(w+s+1)+sin(2*%pi*f*t)*0.1; end sound(x,44100);さて、このプログラムでは音が半音階的にずれていくので、あまり音楽的ではない。
そこでドレミの音階らしくしてみよう。
そのためには半音的な音を除いてピアノの白鍵の音だけを演奏すればよい。ピアノの白鍵と音の高さの関係は図のようになっている。
nを半音毎の音の高さとすると音名iとnと周波数の関係は以下のようになる。
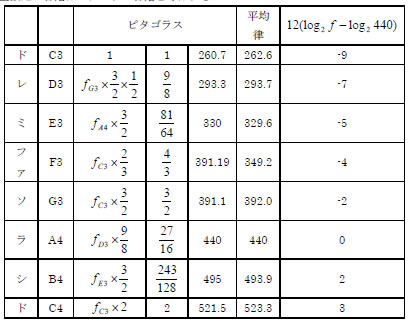
ドレミ 音名 i n 計算式 周波数 ラ A4 0 0 440×2^(0/12) 440 シ B4 1 2 440×2^(2/12) 493.8 ド C5 2 3 440×2^(3/12) 523.3 レ D5 3 5 440×2^(5/12) 587.3 ミ E5 4 7 440×2^(7/12) 659.3 ファ F5 5 8 440×2^(8/12) 698.5 ソ G5 6 10 440×2^(10/12) 784.0 ラ A5 7 12 440×2^(12/12) 880 シ B5 8 14 440×2^(14/12) 987.8 ド C6 9 15 440×2^(15/12) 1046.5 scilabでは小数点以下を切り捨てるintという関数があり、たとえば int(3.2),int(3.7), int(3.0)はすべて3になる。
このintを用いるとこの表のiからnを計算で求めることができる。赤文字のようにnとiの換算式を追加すると、ト短調の音階を演奏できる。
stacksize(1e8); fs=44100; x=zeros(1:20*fs); w=0:10000; t=w/fs; for i=0:14 s=i*fs/4; n=int(i/7*12+.4); f=440*2^(n/12); x(w+s+1) = x(w+s+1) + sin(2*%pi*f*t) * .1; end sound(x,44100);ハ長調は2から始めればよいから、以下の赤文字のようにiに2を加算すればハ長調が演奏できる。
stacksize(1e8); fs=44100; x=zeros(1:20*fs); w=0:10000; t=w/fs; for i=0:14 s=i*fs/4; n=int((i+2)/7*12+.4); f=440*2^(n/12); x(w+s+1) = x(w+s+1) + sin(2*%pi*f*t) * .1; end sound(x,44100);
すこし詳しい説明
A4とかG5というのは、音名のアルファベット表記として国際的に使われている表記方法だ。ABCDEFGがピアノの白鍵の1オクターブに相当し、オクターブ毎に下から1,2,3,4という番号がついている。A1がピアノの最も低い鍵盤でA8はそこから7オクターブ上の音になる。
「音名・階名表記」『ウィキペディア日本語版』、
2010年5月24日 (月) 15:10 UTC、
URL http://ja.wikipedia.org/wiki/音名・階名表記
intを使ってiからnを計算する方法を自分で考えることはできただろうか?
音階の場合はiとnの関係はだいたい比例している。そしてiが7増える毎にnは12増えればよい。こうしたことから、まず
n=i/7*12
という式が元になりそうである。このままだと整数にならないので、ここでintを使って、
n=int(i/7*12)
としてみると、だいたいさそうだが、たとえばi=1でn=2となってほしいのだがint(1/7*12)は1になってしまう。
そこで、0.4を加えて
n=int(i/7*12+0.4)
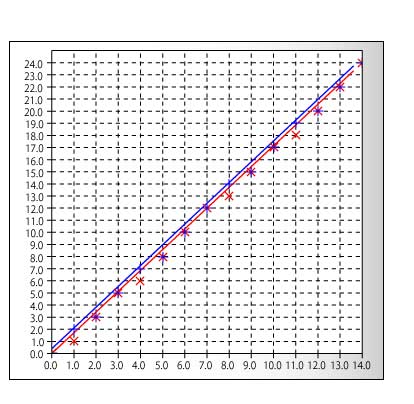
iとnの関係と、i/7*12 および i/7*12+0.4の直線の式をグラフを方眼紙に書いて比較してみよう。