program1 波形が一致する場所を探す

--> program1

波形が完全に一致する場所を探索する

2400サンプル(1msに相当する)おきに波形を比較し、一致する位置を探す

abs, sumを使っている

abs = 絶対値を計算する。複素数にも使える。

例1 abs(-1) -> 1

例2 abs(1 + %i) -> 2^(0.5)

sum = 合計を計算する

例1: sum([1,2,3]) -> 1+2+3 = 6

program1の問題点=誤差に弱い

少しでも誤差があれば波形は一致しない。

program2 誤差が最小の位置を探す

--> program2

2400サンプル(10ms)おきに波形を比較していく。

誤差が最小の位置を探す。

program2の問題点=高い周波数成分に弱い

100Hzのsin信号では10msの誤差はわずかな差にしかならない。

10ms間隔で探索しているから、正解とは5m程度はずれる可能性がある。

たとえば1kHzのsin波形が入っていた場合、program2がどのようになるかを確認してみよう。」

yとして0.1秒の1000Hzのsin信号を作る

xとして、1秒間の無音信号を作る

yの0.5秒の位置にxを挿入する。

program2と同じ方法で分析し、誤差をグラフにして表示する。

// サンプリング周波数 24000
// 1秒の無音の中の0.1秒のsin関数を探す

t1=(1:2400)/24000;
y=sin(2*%pi*1000*t1); // 0.1秒のsin関数
plot(t1,y);
t2=(1:24000)/24000;
x=t2*0;              // 1秒の無音信号
x(12001:(12000+2400))=y; // 0.5秒後に0.1秒のsin関数
figure();
plot(t2,x);
r=0;   // r を 0 で初期化
for i=1:200
    p=i*100
    err=sum(abs(x(p+1:p+2400)-y))
    r(i)=err  // r(i)にi*100サンプルのでの波形差
end
figure();  // 各位置での波形差をプロットする
plot((1:200)*100/22000,r);              

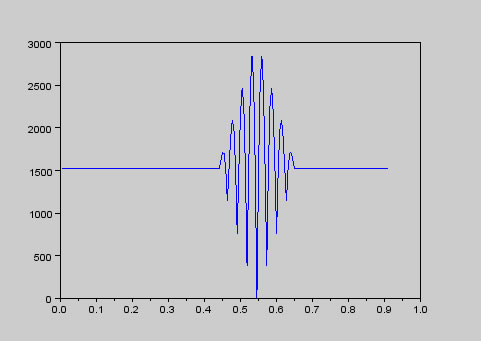
sin関数と波形の誤差は無音部分では1500くらいだ。

sin波がある0.5秒で小さくなるが。

しかし、その前後で誤差が0～3000の間で上下に何度も振れている。これはsin関数とsin関数の差が位相差によっては互いに反対方向の振れになる。そのような場合は同じ1kHzの信号でも波形の差は大きくなってします。