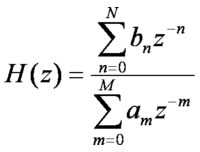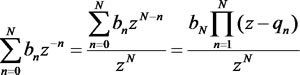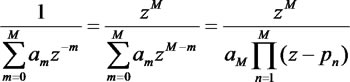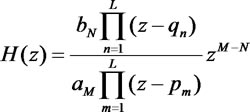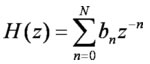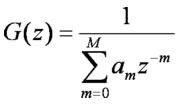零と極
フィルター、部屋の反射など、音が伝わる経路をすべてz変換であらわすことができる。
また、有限個のディレイと演算からなる信号処理は、
という形であらわせる。
ここで、分母だけをとりだして以下のように変形することができる。
まず分数の形にして、分母/分子にz^Nを乗ずると、分母はzの多項式になる。そして、zの多項式を因数分解すれば、(z-q(n))という因数をNこ乗じたものになる。
分母も、同じような方針で因数分解することができるだろう。
これを組み合わせると、けっきょく、分母、分子とも因数分解することができる。そして、L=max(N,M)とすると、H(z)を以下のような形であらわすことができる。
ここで、分母についてみてみると、
の場合、分母は0になるから、H(z)も0になる。
このことが意味するのは、
のどれかと等しいところでは特殊な点で、それらの点ではH(z)は0になるということだ。
これらの点を「零」、または ゼロ(英語では zero)と呼ぶ。
一方、
の場合は、H(z)は無限大いなる。
このことが意味するのは、
のどれかと等しいところでは特殊な点で、それらの点ではH(z)は無限大になるということだ。
これらの点を「極」、英語では pole と呼ぶ。
という形のフィルターは
という形に変形できるが、この形のフィルタは、零しか持っていないので、「全零フィルター」英語では「all zero filter」と呼ぶ。また、
の形のフィルタは
と変形できるが、この場合G(z)は極しか持たないので、全極フィルター、all pole filterなどと呼ぶ。