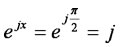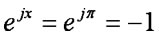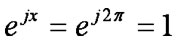複素数の指数関数

指数関数には以下のような性質があるのだった。

そこで、

指数関数≡このような微分方程式の解

と定義しよう。すると、

となる。ということは、

という関数は、もしxが増加した場合に

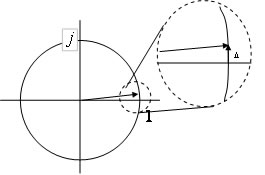
の方向に変化するということだ。これを複素平面で考えてみよう。iを乗ずるということは中心点からの角度に対し90度の方向ということだ。すなわち、このように、中心からの方向に対し、90度の方向にが移動することになる。

したがって、常に円周にそって進む。

このようには半径が1の「円」を描く。これを「単位円」と呼ぶ。

よくわからなくても、実は大丈夫

さて、理屈はやや難しかったと思うが、これは指数関数が円を描くことを納得しやすくするための説明であって、信号処理の問題を解く際に必要な知識ではない。なので、複素数の性質を理解すれば、説明の方は忘れてしまってもかまわない

覚えておいてほしいのは以下のことだけだ。

1) 複素数の掛算、足し算

2) 複素平面の図の見方 (横軸が実数、縦軸が虚数)

3) 複素数の指数関数は半径1の円になる。

4) xの移動量と円周上の長さは同じ。

以上のことがわかっていれば、以下は簡単に導ける。

のとき、

のとき、

のとき、

計算のルールがいったんわかってしまえば、とても簡単だ。

という式を見たら、すぐに複素平面上に単位円を思い浮かべて、xのいろいろな値に対し、単位円上のどの点が対応するか、瞬間的にわかるようになるまでしっかりと覚えてほしい。

練習問題

(1) 複素平面を描け

(2) 指数関数でxが0～2πまで変化した時に描かれる単位円を描け。

(3) 以下の点を複素平面上で示せ