デシベル

Q. 音の大きさはどう表せばよいか?

音の大きさは、「dBspl」であらわす。

dBsplは対数

デシベルは下記の式で計算した数値だ。

P=気圧(単位はパスカル)。

Q: 気圧の変化が 1気圧の2/10万の場合、音の大きさは何dBsplだろうか?

 

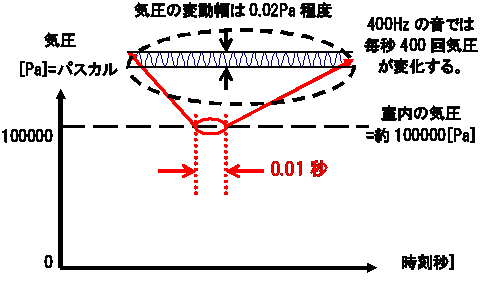
どうしてdBsplは対数

dBsplは音の大きさを対数であらわしている。

利点: ほとんどの大きさの音を2桁で表現できる。

dBSPL	Pa	例
140	200	ジェットエンジン
120	20	耳の損傷が始まる
100	2	映画館の最大音量
80	0.2	普通の音楽
60	0.02	静かな音楽
40	0.002	静かな室内
20	0.0002	ほぼ無音
0	0.00002	無音室の中

たとえば、0.002Paと表すよりも 40dBsplと表す方が扱いやすい。

dBは倍率を表すのにも使われる

dBという単位は「倍率」を表現するのにもよく使われる。たとえば、振幅Aが振幅Bの10倍である場合、振幅Aは振幅Bの+20dBである、と表現する。

振幅 a/ b

20 log　(a/b) / log 10

なぜ対数を使うのか?

対数は倍率の計算に便利だからだ。

たとえば音量は音源の音圧、マイク感度、スピーカー能率に比例するが、以下のA,Bの音量を合わせるには、Bの音量つまみをAに対してどの程度上げればいいだろう?

	A	B
音源	トランペット 0.28Pa	ピアノ 0.2Pa
マイク感度	0.0158(Volt/Pascal)	0.0125(Volt/Pascal)
スピーカー能率	0.4Pa/W	0.316Pa/W

それぞれの数字を掛け合わせるのはちょっとたいへんだ。

しかしすべてdBで表現されていれば、音量差は足し合わせるだけでよい。

	A	B	差
音源	トランペット 83dBspl	ピアノ 80dBspl	-3
マイク感度	-36dB re 1(Volt/Pascal)	-38dB re 1(Volt/Pascal)	-2
スピーカー能率	86dBspl/W	84dBspl/W	-2

AとBの差を足し合わせていけば、AとBの音量差が、-3-2-2= -7dBであることがすぐに計算できる。

対数はこのようにとても便利なものだ。

今すぐ指数関数と対数を復習しよう!

エネルギーのdB値は計算方法が異なる

エネルギーのdB値は計算式が異なる

エネルギー c/d

10 log (c/d) / log 10

エネルギーは振幅の2乗に比例するので、同じ振幅比に対するdB値はどちらの計算方法でも同じになる。

よく使うdB値は覚えてしまおう

エネルギーで2倍の音は+3dB,

10倍の音は+10dB

などのdB値はおぼえておくと大変便利だ。

以下の表のdB値は覚えておくと便利なので、覚えておこう。

振幅	エネルギー	dB
10倍	100倍	+20
約3倍	10倍	+10
約2倍	4倍	+6
約1.4倍	2倍	+3
1/10	1/100	-20
約1/3	1/10	-10
約1/2	1/4	-6
約1/1.4	1/2	-3

 

これだけは覚えよう

Q 音の大きさの単位は? A dBspl

Q 60dBsplの音に対し、以下の音のdB値を求めよ

振幅10倍 -> + 20dB = 80dB

振幅1/10 -> -20dB = 80dB

振幅 2倍 -> 約 +3dB = 83dB

振幅 1/2 -> 約-3dB = 77dB

エネルギー 10倍-> +10dB = 70dB

エネルギー2倍->+3dB = 63dB

エネルギー半分 -> -3dB = 57dB

エネルギー1/10->　-10dB = 50dB

エネルギー 5倍 = 10倍の半分 -> 60+10-3 = 67dB

エネルギー20倍 = 10倍の2倍 -> 60+10+3 = 73dB