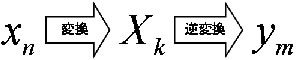DFTとFFT

これからフーリエ変換について学ぶ。

サンプリングされた信号のフーリエ変換はDFT(離散フーリエ変換)と呼ばれ、以下の式で計算することができる。

変換

[式1]

逆変換

[式2]

フーリエ変換をして得た数列を、再度逆フーリエ変換すると、元の信号に戻る。

もしこの計算の結果、x(n)=y(n)になれば、デジタルフーリエ変換し、逆変換すると元の信号に戻ることになる。

以下では scilabを使って、このようにフーリエ変換した結果を再度逆フーリエ変換すると、元の信号に戻ることを確認しよう。

scilabによるフーリエ変換

X(k)のかわりに xxと書くことにする。

xx=fft(x,-1);

注意: xx, yの添え字は1から始まるので、数式とは添え字が1ずれる。

scilabによる逆フーリエ変換

y=fft(xx,1);

注意: xx, yの添え字は1から始まるので、数式とは添え字が1ずれる。

フーリエ変換と逆フーリエ変換の実験

まず適当な数列を作り、それをフーリエ変換して、逆フーリエ変換し、元の数列に戻るかを確認してみよう。

x	元の数列
xx	フーリエ変換の結果
y	xxを逆フーリエ変換した結果

とする。3行目で、x(111)～x(115)に適当な数列を入れている。

w=101:130; x(44100)=0; x(111:115)=[0.7,-0.3,0.5,0.8,-0.4]'; xx=fft(x,-1); y=fft(xx,1);

xとyが同じかどうかを確認しよう。以下は1行づつ実行する。1行目ではx, 2行目ではyがプロットされる。3行目では比較のために, yを +1 上にプロットしているが、完全に同じ波形が再現されていることがわかる。

plot2d(w,x(w)); plot2d(w,y(w)); plot2d(w,[x(w)';y(w)'+1]');

以下のように数値を比べてみても、誤差は非常に小さいことがわかる。

x(110:120) y(110:120)

逆フーリエ変換の誤差は、純粋に計算誤差だけだ。計算精度を上げれば、逆フーリエ変換の結果を限りなく元の値に近づけることができる。