位相

次に sin関数の位置を時間軸に沿って前後に移動した場合、フーリエ変換の結果がどのように変わるかを確認してみよう。

fs=8000; l=16000; n=0:l-1; t=n / fs; x0=fft(sin(2*%pi*440*t),-1); x1=fft(sin(2*%pi*440*t+%pi/2),-1); x2=fft(sin(2*%pi*440*t+%pi),-1); x3=fft(sin(2*%pi*440*t+3*%pi/2),-1);

若干面倒だが、順に見ていこう。

plot2d(n,real(2*x1/l),rect=[0,-1,fs,1]);; plot2d(n,imag(2*x1/l),rect=[0,-1,fs,1]);; plot2d(n,real(2*x2/l),rect=[0,-1,fs,1]);; plot2d(n,imag(2*x2/l),rect=[0,-1,fs,1]);; plot2d(n,real(2*x3/l),rect=[0,-1,fs,1]);; plot2d(n,imag(2*x3/l),rect=[0,-1,fs,1]);; plot2d(n,real(2*x4/l),rect=[0,-1,fs,1]);; plot2d(n,imag(2*x4/l),rect=[0,-1,fs,1]);;

440Hzに対応する実部と虚部の値が以下のようになっている。

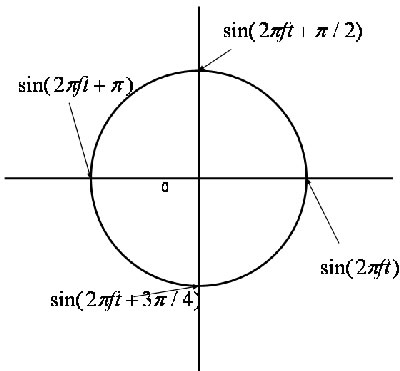
波形	実部	虚部	Phase
sin(x)	1	0	0
sin(x+π/2)	0	1	π/2
sin(x+π)	-1	0	π
sin(x+3π/2)	0	-1	-π/2

 

図にしてみると以下のようになる。

 

 

このように、sin関数のスタート位置(時間方向での移動)は、フーリエ変換の結果では、複素平面上の角度になっていることがわかる。

sin関数の時間方向の位置を、この複素平面の角度で表すことがある。この場合は、「位相」という言葉を使う。たとえば、右チャンネルの信号はπ/2位相が進んでいる、などと表現する。また左右のチャンネルは逆相である、などと表現する。