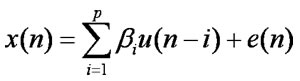MAモデル
MA = Moving Average = 移動平均
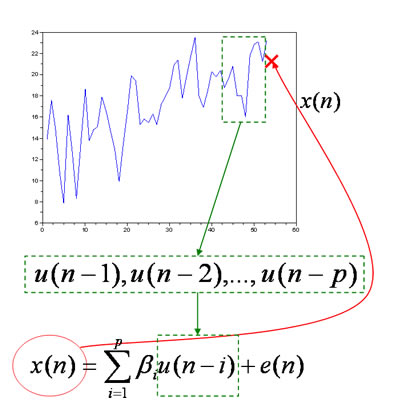
以下は、ある地点の4月から5月までの53日分の毎日の気温である。
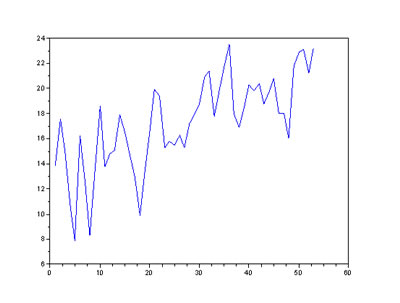
x=[13.9, 17.6, 15.0, 10.7, 7.9, 16.2, 12.4, 8.3, 13.5, 18.6, 13.8, 14.8, 15.1, 17.9, 16.5, 14.8, 13.0, 9.9, 13.2, 16.6, 19.9, 19.4, 15.3, 15.8, 15.5, 16.3, 15.3, 17.2, 17.9, 18.7, 20.9, 21.4, 17.8, 19.9, 21.7, 23.5, 18.0, 16.9, 18.5, 20.3, 19.8, 20.4, 18.8, 19.7, 20.8, 18.0, 18.0, 16.0, 21.8, 22.9, 23.1, 21.2, 23.2 ];
plot(x);
次の日の気温の予想するにはどうすればよいだろうか?
(1) 前の日の気温を次の日の気温の予想値とする
(2) 直前2日の平均を次の日の気温の予想値とする
(3) 直前3日の平均を次の日の気温の予想値とする
これを比較してみよう。
n=4:53;
x0=x(n);
y1=x(n-1);
y2=0.9*x(n-1)+0.1*x(n-2);
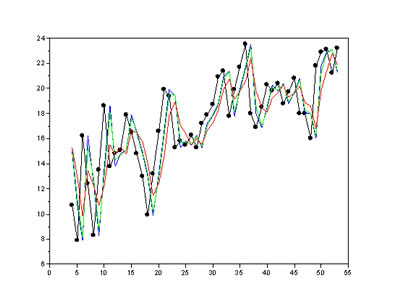
y3=0.6*x(n-1)+0.2*x(n-2)+0.2*x(n-3);これらを予想する値 x(n) と比較してみよう。
plot(n,x0,'bla.-',n,y1,'blu-',n,y2,'gre-',n,y3,'red-');
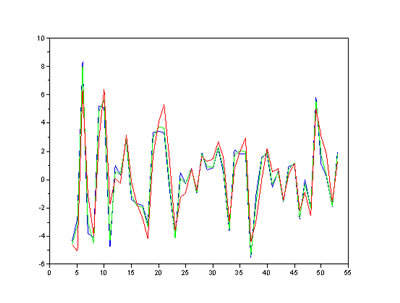
これだけでは、予想の精度がよくわからないから、誤差成分だけをプロットしてみよう。
d1=x0-y1;
d2=x0-y2;
d3=x0-y3;
plot(n,d1,'blu-',n,d2,'gre-',n,d3,'red-');
どうも赤の振幅が若干少ない。誤差を正確に比較するため、誤差の二乗の和をもとめてみよう。
-->sum(d1^2)
ans =412.04
-->sum(d2^2)
ans =408.28
-->sum(d3^2)
ans =388.0536
1番目の予測より2番目が、2番目より3番目の予想の方が精度がよい。
この予測方法は、過去の数サンプルの重み付き平均で予測をすることから、「移動平均」=「Moving Average」と呼ばれている。
一般的な計算式は以下の式になる。
そして、以下のように直前のp個のデータから次のデータを予測する。
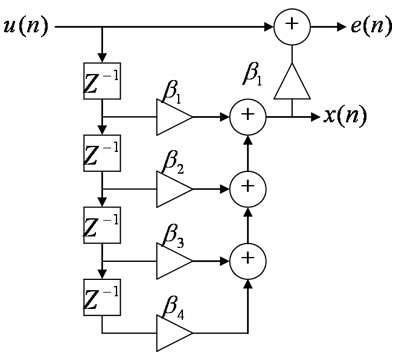
ブロック図にすると以下のようになる。
ここで、
という記号が出てきた。これは1サンプルの遅延をあらわす。
なぜ
