3つの正規形

第1正規形: 繰り返し項目を排除する

第2正規形: 部分関数従属の排除

第3正規形: 推移的関数従属の排除


ちょっと余計に知っておきたい人のうんちく知識

さらに制約を課した「第4正規形」「第5正規形」もある。
正規化の概念は、最初E.F.コッド氏が提唱し定式化した。これはコッド正規形言う。
後にR.F.ボイス氏とE.Fコッド氏により改良された正規型をボイスコッド正規形と言う。

 

正規形でないデータと、3つの正規形のデータがどのように異なるかを、音楽データベースを例にとって見てみよう。

正規形でないデータ

小林推薦曲 倖田 夾未(女性ソロ)の「1000の言葉」、邦楽 raphael「夢より素敵な」, asian ROCK 田村推薦曲 The OFF SPRING,"All I Want", Punk Rock ... .

第1正規形の条件は、くりかえし構造を廃し、テーブル型のデータとすることである。

以下のような形にすれば第1正規形の条件を満たしている。

 

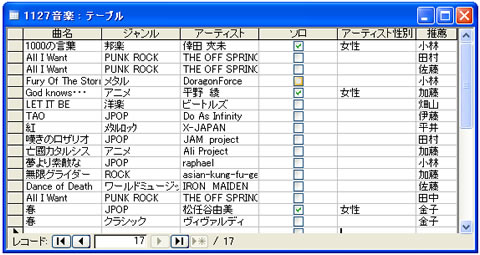
第2正規形の条件は、「部分関数従属の排除」だ。

これは用語は難しいが、ようするに、一つのテーブルのなかのあるフィールドの値から、他のフィールドの値が決まってしまうのであれば、その部分は別のテーブルに移しなさいということだ。上のテーブルでは、アーティスト欄がわかれば、そのアーティストがグループであるか、また性別が女性であるか男性であるかは決まってしまう。この部分を別のテーブルに移動することで第2正規形の条件が満たされる。

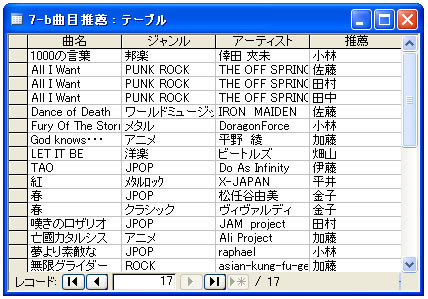
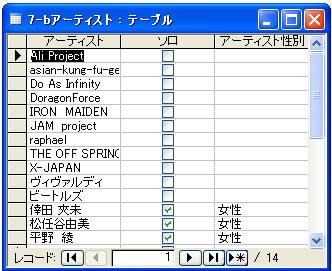
さらに第3正規形とするためには、「推移的関数従属の排除」を行う必要がある。

これもたいへん難しい言葉だが、上のデータをよく見てみると、なんとなく無駄な部分がないだろうか。曲目が決まれば「曲名」「アーティスト」は決まってしまうのに、上の表では何度も同じデータが記載されている。

しかし、これは部分関数従属ではない。ためしに、曲名によって決まる他のデータがあるかどうかを考えてみると、「春」という曲は異なる曲が2曲含まれているので、曲名だけでは楽曲が決まらないから、ジャンルなども決まらないのである。

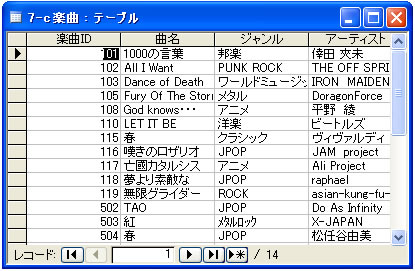
そこで、「楽曲」というデータにはない実体を想定してそれにIDをつけ、「楽曲ID」とすれば、この楽曲IDからは、「曲目」「アーティスト」「ジャンル」などが決まることになる。これが「推移的関数従属」ということだ。

「楽曲ID」というあらたなデータを追加することで、「推移的関数従属」をとりのぞいたのが下のテーブルである。

 

 

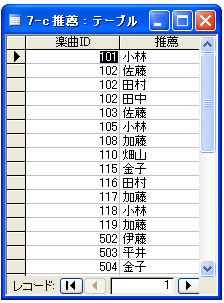
第3正規形の作り方

第1正規形: 繰り返し項目を排除する

第2正規形: 部分関数従属の排除

第3正規形: 推移的関数従属の排除

では判りにくい。そこで第3正規形を作る簡単な方法を黒板で教えよう。

この方法で、響子さんのネットショップを第3正規形にしてみよう。

また以下のようなデータベースを第3正規形にしてみよう。

1 自分の知り合いの趣味、知り合い同士が知り合いかどうか

2